Ln P Vs 1 T
8.5: The Clausius-Clapeyron Equation
- Page ID
- 84340
The Clapeyron equation can exist developed farther for phase equilibria involving the gas stage as one of the phases. This is the case for either sublimation (\(\text{solid} \rightarrow \text{gas}\)) or vaporization (\(\text{liquid} \rightarrow \text{gas}\)). In the case of vaporization, the modify in molar volume can be expressed
\[ \Delta V = V_{gas} -V_{liquid}\]
Since substances undergo a very large increase in molar volume upon vaporization, the molar volume of the condensed phase (liquid in this instance) is negligibly small compared to the molar volume of the gas (i.east., \(V_{gas} \gg V_{liquid}\)). So,
\[\Delta 5 \approx V_{gas}\]
And if the vapor can be treated every bit an ideal gas,
\[V_{gas} = \dfrac{RT}{p}\]
Substitution into the Claperyron equation yields
\[\dfrac{dp}{dT} = \dfrac{p\Delta H_{vap}}{RT^2}\]
Separating the variables puts the equation into an integrable form.
\[dp = \dfrac{p\Delta H_{vap}}{R} \dfrac{dT}{T^2} \label{diffCC}\]
Noting that
\[\dfrac{dT}{T^2} =- d\left(\dfrac{i}{T} \right) \]
makes the integration very piece of cake. If the enthalpy of vaporization is independent of temperature over the range of conditions,
\[ \int_{p_1}^{p_2} \dfrac{dp}{p} = - \dfrac{\Delta H_{vap}}{R} \int_{T_1}^{T_2} d\left(\dfrac{ane}{T} \right) \]
\[ \ln \left( \dfrac{p_2}{p_1}\right) = - \dfrac{\Delta H_{vap}}{R} \left( \dfrac{ane}{T_2} -\dfrac{1}{T_2} \correct) \characterization{CC}\]
This is the Clausius-Clapeyron equation. It can also be used to describe the purlieus betwixt solid and vapor phases by substituting the enthalpy of sublimation (\(\Delta H_{sub}\))
Example \(\PageIndex{1}\):
The vapor pressure of a liquid triples when the temperature is increased from 25 °C to 45 °C. What is the enthalpy of vaporization for the liquid?
Solution:
The trouble tin can be solved using the Clausius-Clapeyron equation (Equation \ref{CC}). The following values can exist used:
| \(p_2 = 3 p_1\) | \(T_2 = 318\, 1000\) |
| \(p_1 = p_1\) | \(T_1 = 298\, K\) |
Substitution into the Clausius-Clapeyron equation yields
\[ \ln \left( \dfrac{3p_1}{p_1}\right) = - \dfrac{\Delta H_{vap}}{ix.314 \dfrac{J}{mol\,K}} \left( \dfrac{i}{318\,One thousand} -\dfrac{i}{298\,Chiliad} \right) \]
\[ \Delta H_{vap} = 43280 \,\dfrac{J}{mol} = 43.28 \, \dfrac{kJ}{mol}\]
The Clausius-Clapeyron equation also suggests that a plot of \(\ln(p)\) vs. \(1/T\) should yield a straight line, the gradient of which is \(–\Delta H/R\) (provided that \(\Delta H_{vap}\) is contained of temperature over the range of temperatures involved..
\[ \ln(p) = - \dfrac{\Delta H_{vap}}{R} \left( \dfrac{ane}{T} \right) + const.\]
This arroyo is very useful when there are several pairs of measurements of vapor pressure and temperature. Such a plot is shown below for h2o.
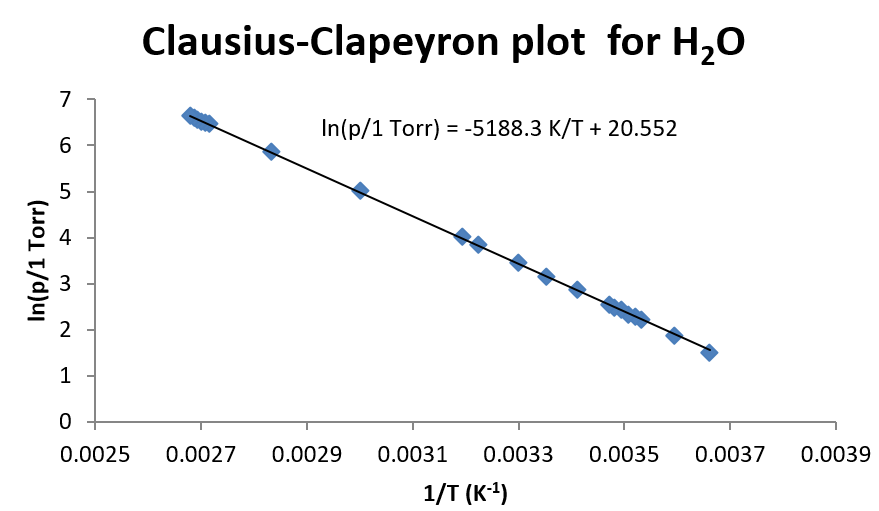
For water, which has a very large temperature dependence, the linear human relationship of \(\ln(p)\) vs. \(1/T\) holds fairly well over a broad range of temperatures. And so even though at that place is some curvature to the data, a straight line fit even so results in a reasonable clarification of the data (depending, of course, on the precision needed in the experiment.) For this fit of the data, \(\Delta H_{vap}\) is plant to be 43.14 kJ/mol.
Temperature Dependence to \(\Delta H_{vap}\)
For systems that warrant it, temperature dependence of \(\Delta H_{vap}\) tin be included into the derivation of the model to fit vapor pressure as a part of temperature. For example, if the enthalpy of vaporization is assumed to have the following empirical form
\[ \Delta H_{vap} = \Delta H_o + aT + bT^ii\]
and substituting it into the differential form of the Clausius-Clapeyron equation (Equation \ref{diffCC}) generates
\[ \dfrac{dp}{p} = \dfrac{\Delta H_o + aT + bT^2}{R} \dfrac{dT}{T^2}\]
or
\[ \dfrac{dp}{p} = \dfrac{\Delta H_o}{R} \dfrac{dT}{T^ii} + \dfrac{a}{R} \dfrac{dT}{T} + \dfrac{b}{R} dT\]
And so the integrated course becomes
\[ \ln (p) = - \dfrac{\Delta H_o}{R} \left(\dfrac{1}{T}\right) + \dfrac{a}{R} \ln T + \dfrac{b}{R} T + constant\]
The results of plumbing equipment these data to the temperature dependent model are shown in the table below.
| \(\Delta H_0\) (J mol-one) | a (J mol-ane Thousand-1) | b (J mol-one Yard-ii) | c |
|---|---|---|---|
| 43080 | 0.01058 | 0.000501 | xx.fifty |
This results in calculated values of \(\Delta H_{vap}\) of 43.xiii kJ/mol at 298 Grand, and 43.15 kJ/mol at 373 M. The results are a petty chip skewed since in that location is no data above 100 oC included in the fit. A larger temperature dependence would be establish if the higher-temperature data were included in the fit.
Ln P Vs 1 T,
Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_%28Fleming%29/08:_Phase_Equilibrium/8.05:_The_Clausius-Clapeyron_Equation
Posted by: coatestherds.blogspot.com


0 Response to "Ln P Vs 1 T"
Post a Comment